Answer:
-1, 2, 6
Explanation:
We have to solve the equation as follows: 1/(x-6) + (x/(x-2)) = (4/(x²-8x+12)).
Now, we have,
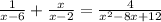
⇒
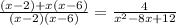
⇒
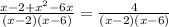
⇒

⇒
![(x-2)(x-6)[(1)/(x^(2) -5x-2) -(1)/(4) ]=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/cpqiju5aq9fozexmwqz3291rck2uzdyqqc.png)
⇒
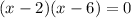 or,
or,
![[(1)/(x^(2) -5x-2) -(1)/(4) ]=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/857iev3ay50hugvt8upo7i72bxvcp9mqgm.png)
If, (x-2)(x-6) =0, then x=2 or x=6
If,
![[(1)/(x^(2) -5x-2) -(1)/(4) ]=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/857iev3ay50hugvt8upo7i72bxvcp9mqgm.png) , then
, then
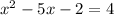
and (x-6)(x+1) =0
Therefore, x=6 or -1
So the solutions for x are -1, 2 6. (Answer)