Question

16. Why is it that momentum is conserved between two objects just before and just after a collision?

Answer 1

Momentum is conserved when the net external force on the system is zero

Step-by-step explanation:

Here we call 'system' the two objects together.

It is possible to demonstrate that the total momentum of a system is conserved when the net external force acting on it is zero. In fact, Newton's second law states that:

`F=ma`

where F is the net external force, m the mass of the system, a its acceleration.

Re-writing the acceleration as rate of change of velocity:

`a=(\Delta v)/(\Delta t)`

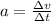
we get:

`F=(m \Delta v)/(\Delta t)`

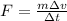
However, assuming that the mass of the system does not change, the quantity at the numerator is just the change in momentum of the system:

`\Delta p = m\Delta v`

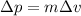
So the equation becomes:

`F=(\Delta p)/(\Delta t)`

And therefore, if the net external force on the system is zero, F = 0, we get

`\Delta p = 0`

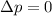
which means that the total momentum is conserved.