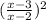Answer:
The lowest form of the fraction is
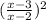
Explanation:
Here, the given equation is
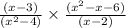
Now, by ALGEBRAIC IDENTITIES, we know that:
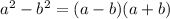
Here,
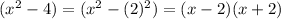
Also,
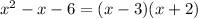 (by splitting the middle term)
(by splitting the middle term)
So, the given expression becomes:
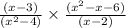 =
=
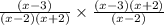
or, the expression becomes
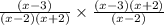
=
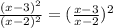
So,the lowest form of the fraction is