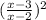Question

Write the rational expression as an equivalent rational expression in lowest terms ((x-3)/(x²-4)). ((x²-x-6)/(x-2)).

Answer 1

The lowest form of the fraction is
`((x-3)/(x-2) )^(2)`

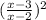
Explanation:

Here, the given equation is

`((x-3))/((x^(2) -4)) * ((x^(2) - x - 6) )/((x-2))`

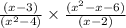
Now, by ALGEBRAIC IDENTITIES, we know that:

`a^(2) - b^(2)  = (a-b)(a+b)`

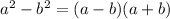
Here,
`( x^(2) -4) = (x^(2)  - (2)^(2) ) = (x-2)(x+2)`

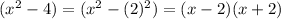
Also,
`x^(2) - x -6 = (x-3)(x+2)` (by splitting the middle term)

So, the given expression becomes:

`((x-3))/((x^(2) -4)) * ((x^(2) - x - 6) )/((x-2))` =
`((x-3))/((x-2)(x+ 2)) * ((x-3)(x+2) )/((x-2))`

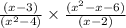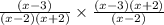
or, the expression becomes
`((x-3))/((x-2)(x+ 2)) * ((x-3)(x+2) )/((x-2))`

=
`((x-3)^(2) )/((x-2)^(2) )  = ((x-3)/(x-2) )^(2)`

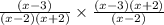
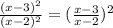
So,the lowest form of the fraction is
`((x-3)/(x-2) )^(2)`