Answer:
x = 4 , x = 9 , x = -5
Explanation:
Given: P(x)=x³-8x²-29x+180
Find the zeros of the polynomial.
First we factor the polynomial and then set each factor to 0.
P(x)=0
Put x=4 into P(x)
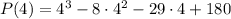
P(4)=0
Divide the polynomial by x-4
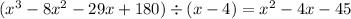
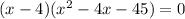
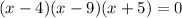
Set each factor to 0
x - 4 = 0 | x - 9 = 0 | x + 5 = 0
x = 4 , x = 9 , x = -5
Zeros of the polynomial, P(x), are -5,4 and 9