Question

Find the GCF of the expression.
3a²+9
A. 3
B. a
C. a+3
D. 3a

Answer 1

3

Explanation:

aaaaaaaaaaaaaaaaaa

Answer 2

Option A

The GCF of the expression
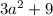`3 a^(2)+9` is 3

Solution:

Need to find GCF of the expression
`3 a^(2)+9`

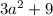
Since only one expression is given it means we need to find G.C.F between two terms

Two terms are
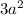`3a^2` and 9.

On factorizing each term we get

`\begin{aligned} 3 a^(2) &=3 * a * a \\ 9 &=3 * 3 \end{aligned}`

So greatest common factor between two term is 3.

so expression can be rewritten as
`3\left(a^(2)+3\right)`

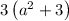
GCF of the terms in an expression helps us in factorization of the expression.

Required solution of G.C.F of expression
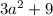`3 a^(2)+9` is option A. that is 3