Answer:
P(x)=(x-2)(x-4)(x+3)(x+6)
Explanation:
Given: P(x)=x⁴+3x³-28x²-36x+144
It is a polynomial with degree 4.
It should maximum four factor.
Hit and trial error method.
Put x = 2 into P(x)
P(2)=2⁴+3×2³-28×2²-36×2+144
P(2) = 0
So, x-2 would be factor of P(x)
Now divide x⁴+3x³-28x²-36x+144 by x-2 to get another factors
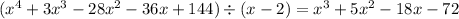
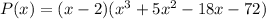
Put x = 4

now divide
 by x-4
by x-4
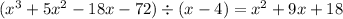
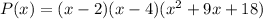
Now factor
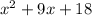


Complete factor of P(x)
P(x)=(x-2)(x-4)(x+3)(x+6)