Question

Consider the polynomial P(x)=x⁴+3x³-28x²-36x+144. Write the equation of P in factored form.

Answer 1

P(x)=(x-2)(x-4)(x+3)(x+6)

Explanation:

Given: P(x)=x⁴+3x³-28x²-36x+144

It is a polynomial with degree 4.

It should maximum four factor.

Hit and trial error method.

Put x = 2 into P(x)

P(2)=2⁴+3×2³-28×2²-36×2+144

P(2) = 0

So, x-2 would be factor of P(x)

Now divide x⁴+3x³-28x²-36x+144 by x-2 to get another factors

`(x^4+3x^3-28x^2-36x+144)/ (x-2) = x^3+5x^2-18x-72`

`P(x)=(x-2)(x^3+5x^2-18x-72)`

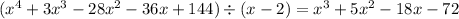
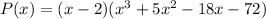
Put x = 4

`P(4) = 0`

now divide
`x^3+5x^2-18x-72` by x-4

`(x^3+5x^2-18x-72)/ (x-4) = x^2+9x+18`

`P(x)=(x-2)(x-4)(x^2+9x+18)`

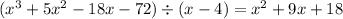
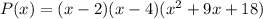
Now factor
`x^2+9x+18`

`\Rightarrow x^2+9x+18`

`\Rightarrow (x+6)(x+3)`

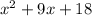
Complete factor of P(x)

P(x)=(x-2)(x-4)(x+3)(x+6)