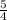Answer:
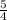
Explanation:
To evaluate :
5x² − 10x
value of x =
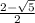
Now,
substituting the value of x in the given equation, we get
⇒
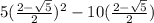
or
⇒
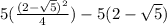
taking 2 - √5 as common, we get
⇒ (2 - √5)
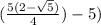
or
⇒ (2 - √5)
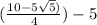
or
⇒ (2 - √5)
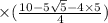
or
⇒ (2 - √5)
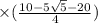
or
⇒ (2 - √5)
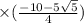
or
⇒
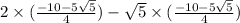
or
⇒
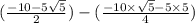
or
⇒
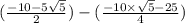
or
⇒
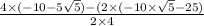
or
⇒
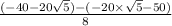
or
⇒
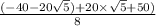
or
⇒
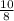
or
⇒