Question

One factor of f(x) = x3 − 12x2 + 47x − 60 is (x − 5). What are the zeros of the function?

5, −4, −3
5, −4, 3
5, 4, −3
5, 4, 3

Answer 1

D) 5, 4, 3

Explanation:

I took the quiz and got a 100%

Answer 2

The correct option is D) 5, 4, 3

Explanation:

Consider the provided function.

`f(x) = x^3 -12x^2 + 47x - 60`

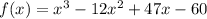
It is given that one factor is (x-5) and we need to find the zeros of the function.

That means x-5 will completely divide the provided polynomial.

`(x^3 -12x^2 + 47x - 60)/(x-5)`

The long division is shown in figure below.

`(x^3-12x^2+47x-60)/(x-3)=x^2-7x+12`

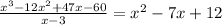
Simplify the expression
`x^2-7x+12`

`x^2-4x-3x+12`

`x(x-4)-3(x-4)`

`(x-4)(x-3)`

`(x-4)(x-3)`

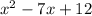
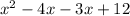
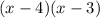
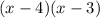
Therefore, the required polynomial can be written as:
`f(x)=(x-3)(x-4)(x-5)`

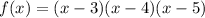
Now find the zeros by substituting f(x)=0.

`(x-3)(x-4)(x-5)=0`

`x-3=0\ or\ x-4=0\ or\ x-5=0`

`x=3\ or\ x=4\ or\ x=5`

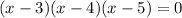
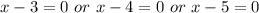
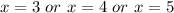
Hence, the correct option is D) 5, 4, 3