Answer:
LHS =
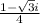 = RHS =
= RHS =
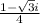
Explanation:
Data provided in the question:
a = −1 + √3i and b = 2
to prove:
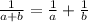
Considering the LHS
⇒
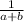
substituting the value of a and b, we get
⇒
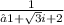
or
⇒
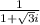
on multiplying and dividing by conjugate ( 1 - √3i )
we get
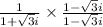
or
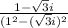
or
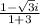 (as (√i)² = -1 )
(as (√i)² = -1 )
or
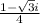
Now,
considering the RHS
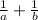
substituting the value of a and b, we get
⇒
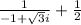
or
⇒
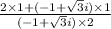
or
⇒
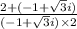
or
⇒
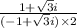
now,
on multiplying and dividing by conjugate ( -1 - √3i )
we get
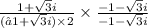
or
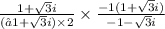
or
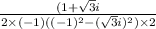
or
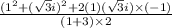
or
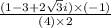
or
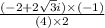
or
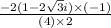
or
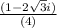
Since, LHS = RHS
hence satisfied