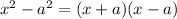Question

Explain the relationship between the polynomial identities: x^2 − 1 = (x +1)(x − 1) and x^2 − a^2 =(x − a)(x +a).

Answer 1

So these two equation can be related by identity
`x^2-a^2=(x+a)(x-a)`

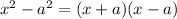
Explanation:

We have given equation
`x^2-1=(x+1)(x-1)`

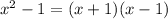
And
`x^2-a^2=(x+a)(x-a)`

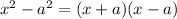
We know the algebraic identity
`a^2-b^2=(a+b)(a-b)`

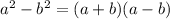
From this identity

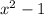`x^2-1` can be written as (x+1) (x-1)

And using same identity
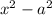`x^2-a^2` can be written as
`(x-a)(x-b)`

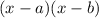
So these two equation can be related by identity
`x^2-a^2=(x+a)(x-a)`