Answer:
The reasons for each statement are show below.
Explanation:
We need to prove (2x)³ is equivalent to 8x³.
Commutative property: According to the commutative property of multiplication
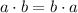
Associative property: According to the associative property of multiplication
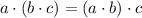
The given expression (2x)³ can be written as
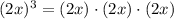
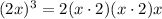 (Associative property)
(Associative property)
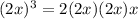 (Commutative property)
(Commutative property)
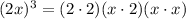 (Associative property)
(Associative property)
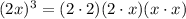 (Commutative property)
(Commutative property)
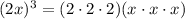 (Associative property)
(Associative property)
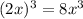
Hence proved.