Question

Which value of x makes the open sentence true?

26−x2>4x−20
8

7

6

5

Answer 1

I hope it helps you get it right

Answer 2

First of all, it might be convenient to rewrite the inequality as

`26-x^2>4x-20 \iff x^2+4x-46<0`

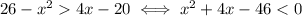
Then, we can plug the proposed value to see which one satisfies the inequality: we want the expression to evaluate to a negative value.

x=8:

`x^2+4x-46 \implies 64+32-46 = 50>0`

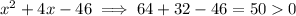
x=7

`x^2+4x-46 \implies 49+28-46 = 31>0`

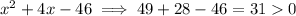
x=6

`x^2+4x-46 \implies 36+24-46 = 14>0`

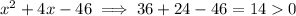
x=5

`x^2+4x-46 \implies 25+20-46 = -1<0`

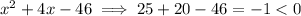
So, the only value that returns a negative value is x = 5.