First of all, it might be convenient to rewrite the inequality as
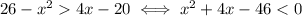
Then, we can plug the proposed value to see which one satisfies the inequality: we want the expression to evaluate to a negative value.
x=8:
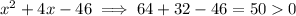
x=7
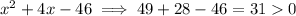
x=6
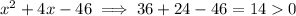
x=5
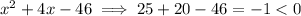
So, the only value that returns a negative value is x = 5.