Question

"ou have discovered another alien. Find the correct

escue path before answering this question.
Which statements are true about the equation of the
ine used to save this alien?
The y-intercept is not visible on the graph
The slope does not exist for this line.
The y-intercept is positive.
The line crosses the x-axis at -3.

Answer 1

A, and D

Explanation:

I got it right on edge.

Answer 2

Correct options are A and D.

Explanation:

From the given graph it is clear that the spaceship is located at (-4,3). The alien is at (-2, -3).

If a line passes through two points
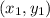`(x_1,y_1)` and
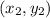`(x_2,y_2)`, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

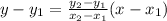
The equation of line is

`y-3=(-3-3)/(-2-(-4))(x-(-4))`

`y-3=(-6)/(2)(x+4)`

`y-3=-3(x+4)`

`y-3=-3x-12`

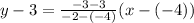
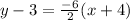
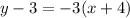
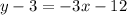
Add 3 on both sides.

`y=-3x-12+3`

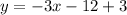
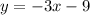`y=-3x-9` .... (1)

Slope intercept form of a line is

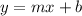`y=mx+b` .... (2)

where, m is slope and b is y-intercept.

On comparing (1) and (2) we get

`m=-3,b=-9`

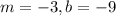
It means,

Slope = -3

y-intercept = -9

Points from -6 to 6 are labeled on y-axis. The y-intercept is -9, so it is not visible on the graph. Option A is correct.

Substitute y=0 in equation (1) to find the x-intercept.

`0=-3x-9`

`3x=-9`

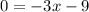
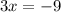
Divide both sides by 3.

`x=-3`

x-intercept is -3. It means the line crosses the x-axis at -3. Option D is correct.