Answer:
Geometric
Exponential
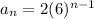
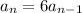 with
with
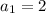
Explanation:
Arithmetic sequences have a common differences.
This is not arithmetic because 12-2 is not the same as 72-12. One is 10 while the other is 60.
Geometric sequences have a common ratio.
This is geometric because 12/2 is the same as 72/12. They are both 6.
Arithmetic sequences are linear.
Geometric sequence are exponential.
Since this is a geometric sequence, then is is exponential.
 means first term.
means first term.
![a_(n-1)[tex] means the previous term to [tex]a_1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6tplyuyfoha5gtxxat2a0jrc01jvfd9qai.png) .
.
The arithmetic sequences have explicit form:
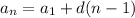
The arithmetic sequences have recursive form:
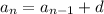 with
with
 given.
given.
 represents the common difference.
represents the common difference.
The geometric sequences have explicit form:
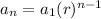
The geometric sequences have recursive form:
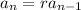 with
with
 given.
given.
 is common ratio.
is common ratio.
So since it geometric, then the explicit formula is
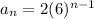 and the recursive form is
and the recursive form is
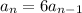 with
with
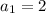 .
.