Answer:
7.2 in
Explanation:
Let length of side of flag=x
Hypotenuse of right triangle=x+3
According to question information
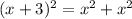
Using Pythagoras theorem
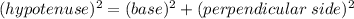
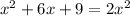
Using identity:
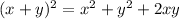

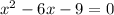
Using quadratic formula :
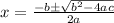
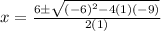
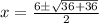
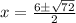


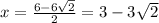
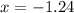
It is not possible because the length of side is always positive.
Hence, the side of flag=7.2 in