Question

for a set amount of time, the distance kirk can run is directly related to his average speed. if kirk can run 3 miles while running 6 miles per hour, how far can he run in the same amount of time if his speed increases to 10 miles per hour?

Answer 1

The amount of time it took him to run 3 miles at 6 mph is 30 minutes

If Kirk ran 10 mph for a full hour, he would travel 10 miles. Since he only runs for half that, he would travel 5 miles

Answer 2

5 miles.

Explanation:

We have been given that for a set amount of time, the distance Kirk can run is directly related to his average speed. Kirk can run 3 miles while running 6 miles per hour. We are asked to find the distance covered if his speed increases 10 miles per hour in same time.

`\text{\text{Time}}=\frac{\text{Distance}}{\text{Speed}}`

`\text{\text{Time}}=\frac{3\text{ Miles}}{\frac{\text{6 miles}}{\text{Hour}}}`

`\text{\text{Time}}=\frac{3\text{ Miles}}{\text{6 miles}}* \text{Hour}`

`\text{\text{Time}}=0.5 \text{Hour}`

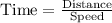
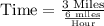
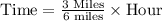
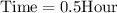
Now, we need to find distance covered at a rate of 10 miles per hour in 0.5 hour.

`\text{Distance}=\text{\text{Time}}* \text{Speed}`

`\text{Distance}=\text{\text{0.5 hour}}* \frac{\text{10 miles}}{\text{Hour}}`

`\text{Distance}=0.5* \text{10 miles}`

`\text{Distance}=5\text{ miles}`

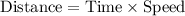
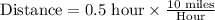
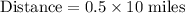
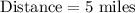
Therefore, Kirk can run 5 miles in same amount of time at a rate of 10 miles per hour.