Answer:
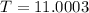 s
s
Step-by-step explanation:
From the question we are told that
The outer ring with a radius of 30 m
inner Gravity Approximately 9.80 m/s'
Outer Gravity Approximately 5.35 m/s.
Generally the equation for centripetal force is given mathematically as
Centripetal acceleration enables Rotation therefore?
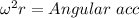
Considering the outer ring,
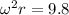
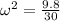
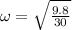
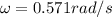
Therefore solving for Period T
Generally the equation for solving Period T is mathematically given as
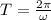
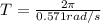
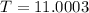 s
s