Question

An FCC iron–carbon alloy initially containing 0.35 wt% C is exposed to an oxygen-rich and virtually carbon-free atmosphere at 1400 K (1127 °C). Under these circumstances the carbon diffuses from the alloy and reacts at the surface with the oxygen in the atmosphere; that is, the carbon concentration at the surface position is maintained essentially at 0 wt% C. (This process of carbon depletion is termed decarburization.) At what position will the carbon concentration be 0.15 wt% after a 10-h treatment? The value of D at 1400 K is 6.9 x 10-11 m2 /s. g

Answer 1

3.99 mm

Step-by-step explanation:

To treat a diffusive process in function of time and distance we need to solve 2nd Ficks Law. This a partial differential equation, with certain condition the solution looks like this:

`\frac{C_(s)-C_(x)}{C_(s)-C{o}} =erf(x/2√(D*t))`

Where Cs is the concentration in the surface of the solid

Cx is the concentration at certain deep X

Co is the initial concentration of solute in the solid

and erf is the error function

First we need to solve the Cs-Cx/Cs-Co on the left to search the corresponding value later on a table.

`(0.15)/(0.35) =0.4285`

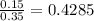
We look on a table and we see for erf(z)=0.4284 z=0.40

Then we solve for x

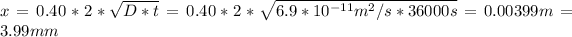`x=0.40*2*√(D*t)=0.40*2*\sqrt{6.9*10^(-11)m^(2)/s*36000s}=0.00399m=3.99mm`t} )[/tex]