Answer:

Explanation:
Given data:
variables deceleration follow as
H - Home - Games
W - Winning Games
from the information we have
P(H) = 0.67
P(W)= 0.30

Need to calculate the percentage of games that win at home. i.e.
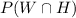
we know that:
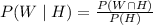
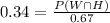
therefore we have
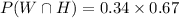
= 0.228
