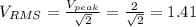Answer:
The amplitude of the voltage source is 2.
The frequency of the voltage in rad/s is 60.
The phase of this voltage source is 45 degrees.
The period is
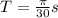
The frequency in Hz is
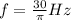
The RMS voltage of the voltage source is 1.41V.
Step-by-step explanation:
Any sinodal function has amplitude 1 when not multiplied by a coefficient c. Here we have
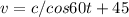 , in which
, in which
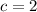 . So, the amplitude is 2.
. So, the amplitude is 2.
For a function
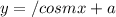 , the period is given by the following formula:
, the period is given by the following formula:
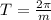 . For this problem, we have a period of:
. For this problem, we have a period of:
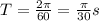
In voltage source in the format
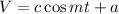 , the phase is a. So, for this voltage source, the phase is 45 degrees.
, the phase is a. So, for this voltage source, the phase is 45 degrees.
The frequency, in Hz, is given by the following function.
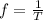
So
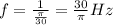
To convert to rad/s, we solve the following rule of three.
1Hz -
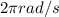

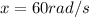
The RMS voltage is given by the following formula:

This voltage source has amplitude 2, so