Answer:
No, those vectors do not span P₂
Explanation:
At first, notice we have 4 vectors from a vector space of dimension 3 ({1,x,x²} is the standard base of P₂) so we are sure they are linearly dependent (because there are more than 3 vectors) i.e. it´s possible to write one of them in terms of other in the same set:
p4=p1-p2
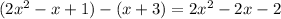
Now, we conclude the span {p1,p2,p3,p4} = {p1,p2,p3}
If we want to know the subspace that this span gets, we work with the matrix of the vectors made as follows:
![A=\left[\begin{array}{ccc}1&3&5\\-1&1&-1\\2&0&4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/io6qdbaw7nnm05h57uhq3knhsrpikscon3.png)
The row-reduction of this matrix show us the basis of the same row-subspace even in the case that some of them are linearly dependent:
![A\ is\ row--equivalent\ to:\left[\begin{array}{ccc}1&0&(1)/(2)\\0&1&-(3)/(2)}\\0&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/2zyo1nd158uvbw1l5316yjvrb4h53e6xx7.png)
This shows that the span {p1,p2,p3}={(1+0.5x²),(x-1.5x²)}
Looking in the previous equality, the span {p1,p2,p3} is generated by two linearly independent vectors, but P₂ needs 3 linearly independent vectors to be generated.
The answer is that {p1,p2,p3,p4}⊂P₂.