Answer:
a) There is an 81% probability that a California adult is an internet user, given that he or she is a college graduate.
b) There is a 68% probability that a randomly chosen internet user is a college graduate.
Step-by-step explanation:
The best way to solve this problem is building the Venn Diagram of these sets.
I am going to say that
A is the percentage of California adults that are college graduates.
B is the percentage of California adults that are regular internet users.
We have that:
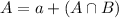 .
.
In which a are those who are only college graduates and
 are those who are both college graduates and regular internet users.
are those who are both college graduates and regular internet users.
By the same logic, we have that:
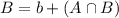
In which b are those who are only regular internet users and
 are those who are both college graduates and regular internet users.
are those who are both college graduates and regular internet users.
We start finding these values from the intersection:
It is also estimated that 21% of California adults are both college graduates and regular internet users. This means that
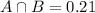
26% of all California adults are college graduates. This means that
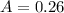
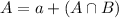
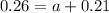
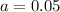
31% of California adults are regular internet users. This means that
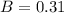
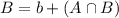
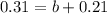
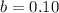
(a) What is the probability that a California adult is an internet user, given that he or she is a college graduate?
The set of college graduates and regular internet users is given by
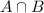 .
.
The set of college graduates is given by
 .
.
So
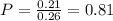
There is an 81% probability that a California adult is an internet user, given that he or she is a college graduate.
b) Among California adults, what is the probability that a randomly chosen internet user is a college graduate?
The set of college graduates and regular internet users is given by
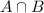 .
.
The set of internet users in given by
 .
.
So
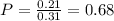
There is a 68% probability that a randomly chosen internet user is a college graduate.