Question

The total surface area for the Asia consisting of forest, cultivated land, grass land, and desert is approximately 4.46 x 107 km2. Every year, the mass of carbon fixed by photosynthesis by vegetation covering this land surface according to reaction 6 CO2(g) + 6H2O (l)  C6H12O6(s) + 6O2(g) is about 455 x 103 kg km-2. Calculate the annual enthalpy change resulting from the photosynthetic carbon fixation over the land surface. Assume 1 bar and 298 K.

Answer 1

Step-by-step explanation:

We calculate the amount of carbon fixed as follows.

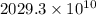`455 * 10^(3) kg/km^(2) * 4.46 * 10^(7) km^(2)`

=
`2029.3 * 10^(10)` kg

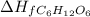`\Delta H_(f)_{C_(6)H_(12)O_(6)}` = -1273.1 kJ/mol

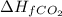`\Delta H_(f)_{CO_(2)}` = -393.5 kJ/mol

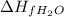`\Delta H_(f)_{H_(2)O}` = -285.8 kJ/mol

Hence, total
`\Delta H` reaction will be as follows.

`\Delta H_(rxn) = (\Delta H_(f)_{C_(6)H_(12)O_(6)}) - 6(\Delta H_(f)_{CO_(2)}) - 6(\Delta H_(f)_{H_(2)O})`

=
`-1273.1 kJ/mol - (6 * 393.5 kJ/mol) - (6 * 285.8 kJ/mol)`

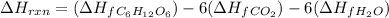
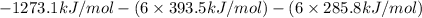
= 2802.7 kJ/mol

Therefore, calculate the number of moles of fixed carbon as follows.

`n_(c, fixed) = \frac{m_(c, fixed)}{\text{Molar mass of C in kg/mol}}`

=
`(4.55 * 10^(5)kg km^(-2) year^(-1))/(12.01 * 10^(-3) kg/mol)`

=
`3.786 * 10^(7) mol km^(-2) year^(-1)`

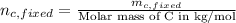
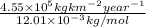
Thus, we can conclude that the annual enthalpy change resulting from the photosynthetic carbon fixation over the land surface is
`3.786 * 10^(7) mol km^(-2) year^(-1)`.