Answer:
The two diameters that separate the top 7% and the bottom 7% are 5.6692 mm and 5.5508 mm respectively .
Explanation:
Given :Mean = 5.61 millimeters
Standard deviation = 0.04 millimeters.
To Find : Find the two diameters that separate the top 7% and the bottom 7%
Solution :
Case 1
We need to find
 such that
such that

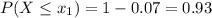
Refer the z table for z value
So, z corresponding to p = 0.97 is 1.48
Formula :
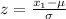
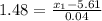
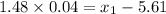

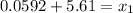

So, the diameter that separate the top 7% is

Case 2)
We need to find
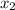 such that
such that
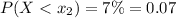
Refer the z table for z value
So, z corresponding to p = 0.07 is -1.48
Formula :
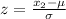
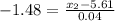
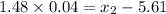
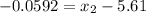
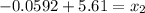
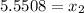
So, the diameter that separate the bottom 7% is
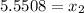
Hence the two diameters that separate the top 7% and the bottom 7% are 5.6692 mm and 5.5508 mm respectively .