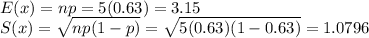Question

Assume that 63% of people are left-handed. If we select 5 people at random, find the probability of each outcome described below, rounded to four decimal places: a. There are some lefties ( ≥ 1) among the 5 people. b. There are exactly 3 lefties in the group. c. There are at least 4 lefties in the group. d. There are no more than 2 lefties in the group. e. How many lefties do you expect? f. With what standard deviation?

Answer 1

a. 0.9931

b. 0.3423

c. 0.3907

d. 0.2670

e. 3.15

f. 1.0796

Explanation:

The probability of the variable that said the number of left-handed people follow a Binomial distribution, so the probability is:

`P(x)=nCx*p^(x)*(1-p)^(n-x)`

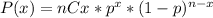
nCx is calculated as:

`nCx=(n!)/(x!(n-x)!)`

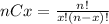
Where x is the number of left-handed people, n is the number of people selected at random and p is the probability that a person is left--handed. So P(x) is:

`P(x)=5Cx*0.63^(x)*(1-0.63)^(5-x)`

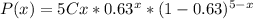
Then the probabilities P(0), P(1), P(2), P(3), P(4) and P(5) are:

`P(0)=5C0*0.63^(0)*(1-0.63)^(5-0)=0.0069`

`P(1)=5C1*0.63^(1)*(1-0.63)^(5-1)=0.0590`

`P(2)=5C2*0.63^(2)*(1-0.63)^(5-2)=0.2011`

`P(3)=5C3*0.63^(3)*(1-0.63)^(5-3)=0.3423`

`P(x)=5C4*0.63^(4)*(1-0.63)^(5-4)=0.2914`

`P(x)=5C5*0.63^(5)*(1-0.63)^(5-5)=0.0993`

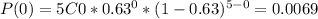
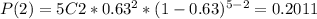
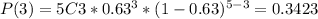
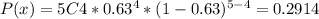
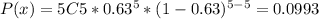
Then, the probability P(x≥1) that there are some lefties among the 5 people is:

P(x≥1) = P(1) + P(2) + P(3) + P(4) + P(5)

P(x≥1) = 0.0590 + 0.2011 + 0.3423 + 0.2914 + 0.0993 = 0.9931

The probability P(3) that there are exactly 3 lefties in the group is:

P(3) = 0.3423

The probability P(x≥4) that there are at least 4 lefties in the group is:

P(x≥4) = P(4) + P(5) = 0.2914 + 0.0993 = 0.3907

The probability P(x≤2) that there are no more than 2 lefties in the group is:

P(x≤2) = P(0) + P(1) + P(2) = 0.0069 + 0.0590 + 0.2011 = 0.2670

On the other hand, the expected value E(x) and standard deviation S(x) of the variable that follows a binomial distribution is:

`E(x)=np=5(0.63)=3.15\\S(x)=√(np(1-p))=√(5(0.63)(1-0.63))=1.0796`