Question

A tank with a capacity of 800 L is full of a mixture of water and chlorine with a concentration of 0.025 g of chlorine per liter. In order to reduce the concentration of chlorine, fresh water is pumped into the tank at a rate of 8 L/s. The mixture is kept stirred and is pumped out at a rate of 20 L/s. Find the amount of chlorine in the tank as a function of time. (Let y be the amount of chlorine in grams and t be the time in seconds.)

Answer 1

The amount of chlorine in the tank as a function of time is
`y=\frac{\sqrt[3]{25}\left(-3t+200\right)^{(5)/(3)}}{1000}`

Explanation:

Let y(t) be the amount of chlorine in grams and t be the time in seconds.

From the information given,

• At time t = 0, there is 20 g of chlorine
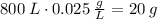  `800 \:L\cdot 0.025\:(g)/(L) = 20 \:g`so the initial condition is y(0) = 20.

• Every second 8 L of freshwater comes in and 20 L of the solution is expelled. This means that for each second that passes, the volume decreases by 12 L.

The main equation that we will be using to model this situation is:

Rate of change of
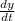`(dy)/(dt)` = Rate of Cl in - Rate of Cl out where

Rate of Cl in = (flow rate of liquid entering) x (concentration of chlorine (Cl) in liquid entering)

Rate of Cl out = (flow rate of liquid exiting) x (concentration of chlorine (Cl) in liquid exiting)

`(dy)/(dt)=(0 \:(g)/(L)) (8 \:(L)/(s))-((y)/(800-12t) )(20 \:(L)/(s))\\(dy)/(dt)=-(20y)/(800-12t)`

`\mathrm{Rewrite\:in\:the\:form\:of\:a\:first\:order\:separable\:ODE}`

`(dy)/(dt)=-(20y)/(800-12t)=-(4)/(4) ((5y)/(200-3t)) \\\\(dy)/(dt)=-(5y)/(200-3t)\\\\(1)/(y)dy= -(5)/(200-3t)dt\\\\\int (1)/(y)dy= \int-(5)/(200-3t)dt\\\\\ln \left(y\right)=(5)/(3)\ln \left(200-3t\right)+c_1\\\\\mathrm{Isolate}\:y:\quad y=e^(c_1)\left(200-3t\right)^{(5)/(3)}\\\\y=c_1\left(200-3t\right)^{(5)/(3)}`

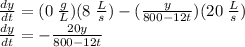
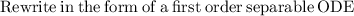
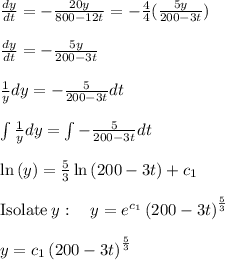
Using the initial condition y(0) = 20

`20=c_1\left(200-3\left(0\right)\right)^{(5)/(3)}\\c_1=\frac{20}{\left(200-3\left(0\right)\right)^{(5)/(3)}} \\c_1=\frac{1}{200\cdot \:5^{(1)/(3)}}`

Substituting

`y=(\frac{1}{200\cdot \:5^{(1)/(3)}})\left(200-3t\right)^{(5)/(3)}\\y=\frac{\sqrt[3]{25}\left(-3t+200\right)^{(5)/(3)}}{1000}`