Answer:
The amount of chlorine in the tank as a function of time is
![y=\frac{\sqrt[3]{25}\left(-3t+200\right)^{(5)/(3)}}{1000}](https://img.qammunity.org/2020/formulas/mathematics/college/x7vuxki8pb549cref8yxllk488ie42z4uf.png)
Explanation:
Let y(t) be the amount of chlorine in grams and t be the time in seconds.
From the information given,
- At time t = 0, there is 20 g of chlorine
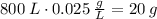 so the initial condition is y(0) = 20.
so the initial condition is y(0) = 20.
- Every second 8 L of freshwater comes in and 20 L of the solution is expelled. This means that for each second that passes, the volume decreases by 12 L.
The main equation that we will be using to model this situation is:
Rate of change of
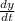 = Rate of Cl in - Rate of Cl out where
= Rate of Cl in - Rate of Cl out where
Rate of Cl in = (flow rate of liquid entering) x (concentration of chlorine (Cl) in liquid entering)
Rate of Cl out = (flow rate of liquid exiting) x (concentration of chlorine (Cl) in liquid exiting)
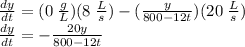
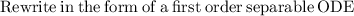
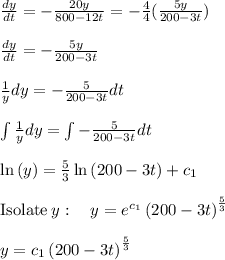
Using the initial condition y(0) = 20
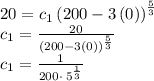
Substituting
![y=(\frac{1}{200\cdot \:5^{(1)/(3)}})\left(200-3t\right)^{(5)/(3)}\\y=\frac{\sqrt[3]{25}\left(-3t+200\right)^{(5)/(3)}}{1000}](https://img.qammunity.org/2020/formulas/mathematics/college/aj9j1a5qwqycow51vwvsnflu4gpsky0hzl.png)