Question

Ray UW is the angle bisector of AngleVUT.

Three lines extend from point U. They are lines U V, U W, and U T.
If mAngleVUW = (4x + 6)° and mAngleWUT = (6x – 10)°, what is the measure of AngleWUT?

32°
38°
48°
76°

Answer 1

AngleWUT =38°, option 2

Explanation:

We have three rays passing through U. A ray is set extend in one direction with one fixed point.

We have UW ray bisecting VUT.As the ray bisects the angle between VUW and WUT would be same .

Given angles are (4x+6)° and (6x-10)°.

As these angles are equal

`4x+6=6x-10`

`2x=16`

`x=8`

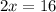
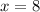
AngleWUT = (6x – 10)°

and x is 8 so on substituting AngleWUT =38°.