Answer:
1a) Length = 7x + 3 & Width = 4x - 2
1b) Area =
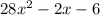
1c) Area = 2774 sq. m
2.
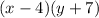
Explanation:
1a)
The length given as words is "3 more than 7 times x"
The width given as words is "4 times x minus 2"
The expression for length would be 7x + 3
The expression for width would be 4x - 2
1b)
The area is length * width
Since we already know the algebraic expressions for length and width from part (a) above, we use the formula:
Area = (7x+3)(4x-2) = 28x^2 -14x + 12x - 6 = 28x^2 -2x -6
Area =
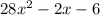
1c)
Given x = 10, we put this into the area expression we found in (b) above.Let's see:
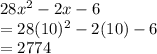
Area = 2774 sq. m
2.
We can group the first two terms and next two terms and write up:
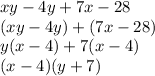
That's the factored form.