Answer:
A)
a= 4.15 m/s² : Magnitude of the acceleration
β= 64.59° : Direction of the acceleration with respect to the horizontal
B)
v = 12.45 m/s : Magnitude of the velocity
β= 64.59°: Direction of the velocity with respect to the horizontal
C)
d = 18.675 m : Magnitude of the displacement
β= 64.59° : Direction of the displacement with respect to the horizontal
Explanation:
A)Data
m=3.2 kg
F₁= (1.9 N)i + (-1.9 N)j
F₂= (3.8 N)i +(-10.1 N)j.
Conceptual analysis
We apply Newton's second law:
∑F = m*a (Formula 1)
∑F : algebraic sum of the forces in Newton (N)
m : mass in kilograms (kg)
a : acceleration in meters over second square (m/s²)
We apply the (Formula 1)
F₁ + F₂= m*a
( (1.9 N)i + (-1.9 N)j)+((3.8 N)i +(-10.1 N)j) = 3.2* a
5.7 i - 12 j = 3.2* a
a=( 5.7/ 3.2) i - (12/3.2) j
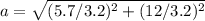
a= 4.15 m/s² : Magnitude of the acceleration

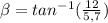
β= 64.59°: Direction of the acceleration with respect to the horizontal
B)-C) Because the object moves with uniformly accelerated movement we apply the following formulas:
vf= v₀+at Formula (2)
d= v₀t+ (1/2)*a*t² Formula (3)
Where:
d:displacement in meters (m)
t : time in seconds (s)
v₀: initial speed in m/s
vf: final speed in m/s
a: acceleration in m/s²
Data
a= 4.15 m/s²
t = 0,
t = 3.0 s
B) we apply the formula (2)
vf= v₀+at
vf= 0+(4.15)(3)
vf= 12.45 m/s :magnitude of the velocity
β= 64.59°: Direction of the velocity with respect to the horizontal
C) we apply the formula (3)
d= v₀t+ (1/2)*a*t²
d= 0+ (1/2)(4.15)(3)²
d=18.675 m :Magnitude of the displacement
β= 64.59°: Direction of the displacement with respect to the horizontal