Question

I graduated from high school and received $1500 in gifts from family

and friends. You also received scholarships in the amount of $800. If you deposit
the total amount received into a 24-month CD at 5.5% compounded daily, how
much will you receive at the end of 24 months?
b. How much interest did you earn on the investment?

Answer 1

Idk but hii

Step-by-step

hiii

Answer 2

At the end of 24 months we will receive $2566.135 as the interest earned on $2300 is $266.135.

SOLUTION:

Given, I graduated from high school and received $1500 in gifts from family and friends. You also received scholarships in the amount of $800.

Total amount received into a 24-month CD at 5.5% compounded daily.

We have to find how much will you receive at the end of 24 months.

Now, amount that is compounded daily is given by:

`\mathrm{A}=\mathrm{a}\left(1+(r)/(n)\right)_{}^{\mathrm{nt}}` → (1)

where A is final amount and a is deposited amount

r is interest rate.

n is number of days

t is number of years

now, a = 1500 + 800 = 2300, r = 5.5%, n = 365 days per year, t =
`(24)/(12)` = 2 years.

Substitute above values in (1)

`\mathrm{A}=2300 *\left(1+((5.5)/(100))/(365)\right)^(365 * 2)`

`\begin{array}{l}{A=2300(1+0.000150)^(730)=2300(1.00015)^(70)} \\ {=2300 * 1.11571=2566.1350}\end{array}`

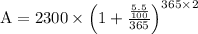
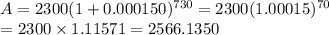
So, in the end we will receive an amount of $2566.135.

Now, interest earned = received amount – deposited amount = 2566.135 – 2300 = $266.135

Hence, at the end of 24 months we will receive $2566.135 as the interest earned on $2300 is $266.135.