Question

A potential customer for an $85,000 fire insurance policy possesses a home in an area that, according to experience, may sustain a total loss in a given year with probability of .001 and a 50% loss with probability .01. Ignoring all other partial losses, what premium should the insurance company charge for a yearly policy in order to break even on all $85,000 policies in this area?

Answer 1

$510

Explanation:

Let X be the amount of money that insurance company will have to pay on the policy for home.

It is given that according to experience, may sustain a total loss in a given year with probability of .001 and a 50% loss with probability .01. Ignoring all other partial losses.

It means the possible values for variable X are 0, 42500 and 85000.

`P(X=42500)=0.01`

`P(X=85000)=0.001`

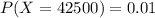
We have only three possible values of X. So,

`P(X=0)+P(X=42500)+P(X=85000)=1`

`P(X=0)=1-0.01-0.001=0.989`

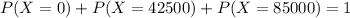
The expected amount of money is

`E(X)=\sum xP(x)`

`E(X)=0\cdot P(X=0)+42500\cdot P(X=42500)+85000\cdot P(X=85000)`

`E(X)=0\cdot (0.989)+42500\cdot (0.01)+85000\cdot (0.001)`

`E(X)=0+425+85`

`E(X)=510`

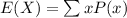
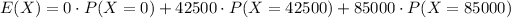
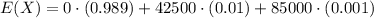
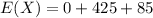
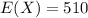
Therefore, the insurance company should charge a premium of $510 for a yearly policy in order to break even on all $85,000 policies in this area.