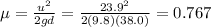Question

You may have noticed runaway truck lanes while driving in the mountains. These gravel-filled lanes are designed to stop trucks that have lost their brakes on mountain grades. Typically, such a lane is horizontal (if possible) and about 38.0 m38.0 m long. Think of the ground as exerting a frictional drag force on the truck. A truck enters a typical runaway lane with a speed of 53.5 mph53.5 mph ( 23.9 m/s23.9 m/s ). Use the work-energy theorem to find the minimum coefficient of kinetic friction between the truck and the lane to be able to stop the truck.

Answer 1

0.767

Step-by-step explanation:

The work done on the truck by the frictional drag force is given by

`W=-Fd`

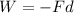
where

F is the magnitude of the frictional force

d = 38.0 m is the maximum displacement allowed for the truck

The negative sign is due to the fact that the force of friction is opposite to the motion of the truck

The force of friction can also be written as:

`F=\mu mg`

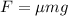
where

`\mu` is the coefficient of kinetic friction between the truck and the lane

m is the mass of the truck

g is the acceleration of gravity

So we can rewrite the work done as

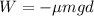`W=-\mu mg d` (1)

According to the work-energy theorem, the work done by friction is equal to the change in kinetic energy of the truck:

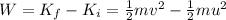`W=K_f - K_i = (1)/(2)mv^2-(1)/(2)mu^2` (2)

where

v = 0 is the final velocity of the truck

u = 23.9 m/s is the initial velocity of the truck

By combining (1) and (2) we get

`-(1)/(2)mu^2 = -\mu mg d`

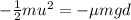
And solving for
`\mu`, we find the minimum coefficient of kinetic friction able to stop the truck in a distance d:

`\mu = (u^2)/(2gd)=(23.9^2)/(2(9.8)(38.0))=0.767`