Question

: Discuss the continuity of the function f(x)=xtan(1/x) at x = 0 given that x≠0 and f(0)=0.

Answer 1

Left hand Limit = Right Hand Limit = f(a)

it is a continuous function.

Explanation:

Solution:

In order to find out the continuity of the function, we need to keep in mind following things:

Left hand Limit = Right Hand Limit = f(a)

Where, f(x) = exists and f(a) = defined.

Data Given:

f(x) = x tan(1/x) x
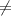`\\eq` 0 (this function is used when x > 0 and x<0)

f(x) = 0 when x = 0

First we have to check the Left hand Limit.

L.H.L = f(0-h) (x<0)

Lim
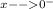`_(x-->0^(-) )` f(x)

Lim
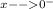`_(x-->0^(-) )` x tan (1/x)

Put x = 0-h

Lim
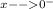`_(x-->0^(-) )` (0-h) tan (1/(0-h))

Lim
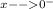`_(x-->0^(-) )` h tan (1/h)

Putting h = 0

(0) x (tan(1/0)))

As we know, for tanx value is a finitely oscillatory between -∞ to +∞

Hence, 0 x finite number then,

L.H.L = 0

Similarly,

R.H.L = f(0+h)

Lim
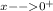`_(x-->0^(+) )` (0+h) tan (1/(0+h))

Lim
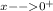`_(x-->0^(+) )` (h) tan (1/(h))

R.H.L = 0

Now, as we know, when x = 0

f(x) = 0

f(0) = 0

Left hand Limit = Right Hand Limit = f(a)

Hence, it is a continuous function.