Answer:
Left hand Limit = Right Hand Limit = f(a)
it is a continuous function.
Explanation:
Solution:
In order to find out the continuity of the function, we need to keep in mind following things:
Left hand Limit = Right Hand Limit = f(a)
Where, f(x) = exists and f(a) = defined.
Data Given:
f(x) = x tan(1/x) x
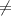 0 (this function is used when x > 0 and x<0)
0 (this function is used when x > 0 and x<0)
f(x) = 0 when x = 0
First we have to check the Left hand Limit.
L.H.L = f(0-h) (x<0)
Lim
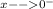 f(x)
f(x)
Lim
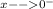 x tan (1/x)
x tan (1/x)
Put x = 0-h
Lim
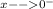 (0-h) tan (1/(0-h))
(0-h) tan (1/(0-h))
Lim
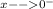 h tan (1/h)
h tan (1/h)
Putting h = 0
(0) x (tan(1/0)))
As we know, for tanx value is a finitely oscillatory between -∞ to +∞
Hence, 0 x finite number then,
L.H.L = 0
Similarly,
R.H.L = f(0+h)
Lim
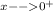 (0+h) tan (1/(0+h))
(0+h) tan (1/(0+h))
Lim
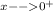 (h) tan (1/(h))
(h) tan (1/(h))
R.H.L = 0
Now, as we know, when x = 0
f(x) = 0
f(0) = 0
Left hand Limit = Right Hand Limit = f(a)
Hence, it is a continuous function.