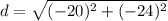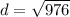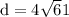Question

Find the distance of AB if point A is A(8,9) and the Midpoint Mis
M(-2, -3).

Answer 1

The distance of AB is
`4√(61)`

Solution:

In the question it is given that the midpoint M is (-2,-3) and point A is (8,9). To find the distance between A and B we have to find the point of B. Let the point of B be
`(x_2,y_2)`

We know,

Mid point for
`x=(x_(1)+x_(2))/(2)`

`\Rightarrow-2=(8+x_(2))/(2)`

`\Rightarrow-4=8+x_(2)`

`\Rightarrow-4-8=x_(2)`

`\Rightarrow-12=x_(2)`

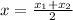
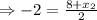
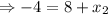
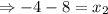
Midpoint
`y=(y_(2)+y_(2))/(2)`

`\Rightarrow-3=(9+y_(2))/(2)`

`\Rightarrow-6=9+y_(2)`

`\Rightarrow-6-9=y_(2)`

`\Rightarrow-15=y_(2)`

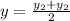
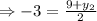
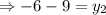
Therefore, the point of B is (-12,-15)

Using the distance formula between two point A and B which is given by

`\mathrm{d}=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

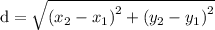
where d is the distance

`d=\sqrt{(-12-8)^(2)+(-15-9)^(2)}`

`d=\sqrt{(-20)^(2)+(-24)^(2)}`

`d=√(400+576)`

`d=√(976)`

`\mathrm{d}=4 √(6) 1`