Question

The equilibrium constant in terms of pressure. Kp for the following process is 0.179 at 50 °C. It increases to 0.669 at 86 °C. C-H16) P C-H16(2) (a) Calculate the molar enthalpy of vaporization (AHvad) of heptane, C-H16 AHvap = kJ mol-1 (b) Calculate the normal boiling point of heptane. Normal boiling point =

Answer 1

a) ΔHvap=35.3395 kJ/mol

b) Tb=98.62 °C

Step-by-step explanation:

Given the reaction:

C₇H₁₆ (l) ⇔ C₇H₁₆ (g)

Kp=P(C₇H₁₆) since the concentration ratio for a pure liquid is equal to 1.

When

T₁=50°C=323.15K ⇒P₁=0.179

T₂=86°C=359.15K ⇒P₂=0.669

The Clasius-Clapeyron equation is:

`ln((P_2)/(P_1)) =-(AH_(vap))/(R) ((1)/(T_2)-(1)/(T_1))`

`ln((0.669)/(0.179)) =-(AH_(vap))/(8.3145 J.mol^(-1)K^(-1)) ((1)/(359.15K)-(1)/(323.15K))`

`1.3184 =-(AH_(vap))/(8.3145 J.mol^(-1)K^(-1)) (-3.10186*10^(-4)K{^-1})`

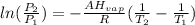
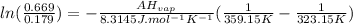
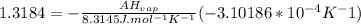
ΔHvap=35339.5 J/mol=35.3395 KJ/mol

Normal boiling point ⇒ P=1 atm

Hence, we find the normal boiling point where:

T₁=323.15K

P₁=0.179 atm

P₂=1 atm

`ln((P_2)/(P_1)) =-(AH_(vap))/(R) ((1)/(T_2)-(1)/(T_1))`

`ln((1atm)/(0.179atm)) =-(35339.5 J/mol)/(8.3145 J.mol^(-1)K^(-1)) ((1)/(T_2)-(1)/(323.15K))`

`1.7203=-4250.34 ((1)/(T_2)-(1)/(323.15K))`

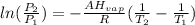
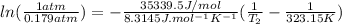
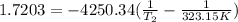
T₂=371.77 K= 98.62 °C