Question

Little’s Law Firm has just one lawyer. Customers arrive randomly at an average rate of 6 per 8 hour workday. Service times have a mean of 50 minutes and a standard deviation of 20 minutes. How long does a customer spend at Little’s Law Firm on average?

a. Approximately one hour
b. Approximately 98 minutes
c. Approximately 75%
d. Approximately 48 minutes

Answer 1

option (b) Approximately 98 minutes

Step-by-step explanation:

Given:

Average arrival rate, λ = 6 per 8 hour or
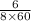`\frac{\textup{6}}{\textup{8}*60}` = 0.0125 / minute

Service Rate, μ =
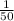`\frac{\textup{1}}{\textup{50}}` = 0.02/min

Standard Deviation = 20 minutes

Now,.

Utilization Rate, ρ =
`(\lambda)/(\mu)`

or

=
`\frac{\textup{0.0125}}{0.02}`

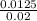
= 0.625

and,

Number of people in Queue =
`(\lambda^2*\sigma^2+\rho^2)/(2*(1-\rho))`

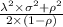
or

=
`(0.0125^2*20^2+0.625^2)/(2*(1-0.625))`

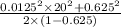
= 0.6042

and,

Waiting in the Queue =
`\frac{\textup{Number of people in Queue}}{\lambda}`

=
`\frac{\textup{0.6042}}{0.0125}`

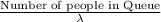
= 48.33 minutes

Thus,

Waiting Time in Office = Wait in the Queue +
`\frac{\textup{1}}{\textup{Service rate}}`

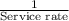
= 48.33 minutes +
`\frac{\textup{1}}{\textup{0.02}}`

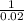
= 48.33 + 50

= 98.33 minutes

hence, the answer is option (b) Approximately 98 minutes