Answer: Option (A) is the correct answer.
Step-by-step explanation:
The given data is as follows.
Work function (
 ) =
) =
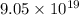 J
J
Now, relation between work function and wavelength is as follows.
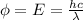
where, h = planck's constant =
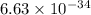 Js
Js
c = speed pf light =
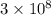 m/s
m/s
 = wavelength
= wavelength
As work function is also known as binding energy. Therefore, putting the given values into the above formula as follows.
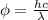
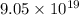 J =
J =

 =
=
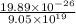
=
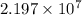
Thus, we can conclude that long wavelength of light which will cause electrons to be emitted is
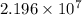 .
.