Step-by-step explanation:
(6.1). The reaction equation will be as follows.
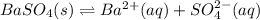
Assuming the value of
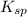 as
as
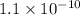 and let the solubility of each specie involved in this reaction is "s". The expression for
and let the solubility of each specie involved in this reaction is "s". The expression for
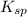 will be as follows.
will be as follows.
![K_(sp) = [Ba^(2+)][SO^(-)_(2)]](https://img.qammunity.org/2020/formulas/chemistry/college/yg34w69sheml5rd0j74pdnlh1afslyrt4i.png) (Solids are nor considered)
(Solids are nor considered)
=
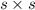
s =
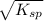
=
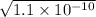
=
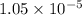
Therefore, solubility of barium sulfate in water is
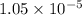 .
.
(6.2). As the molar mass of
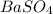 is 233.38 g/mol
is 233.38 g/mol
Therefore, the solubility is g/L will be calculated as follows.
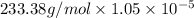
=
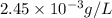
Therefore, solubility of barium sulfate in grams per liter is
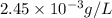 .
.