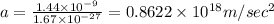Answer:
(A) Acceleration of electron
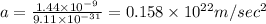
(b) Acceleration of proton
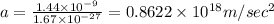
Step-by-step explanation:
We have given distance between proton
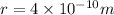
Charge on proton and charge on electron
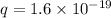
According to coulombs law force between two charge
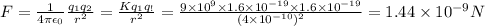
Mass of electron
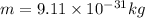
So acceleration of electron
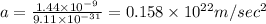
Mass of proton
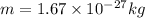
So acceleration of proton