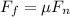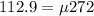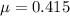Question

(a) In the baggage claim area of an airport, a particular baggage carousel is shaped like a section of a large cone, steadily rotating about its vertical axis. Its surface slopes downward toward the outside, making an angle of 20.5° with the horizontal. A travel bag having mass 30.0 kg is placed on the carousel at a position 7.46 m measured horizontally from the axis of rotation. The travel bag goes around once in 42.0 s. Calculate the force of static friction exerted by the carousel on the travel bag. (Give the magnitude of your answer in N.) (b) The speed of the carousel is adjusted to have a higher constant rotation rate, so that it now makes full rotation every 30.0 s, and the travel bag is bumped to another position, 7.94 m from the axis of rotation. The travel bag is now on the verge of slipping down the sloped surface. Calculate the coefficient of static friction between the travel bag and the carousel.

Answer 1

Part a)

`F_f = 107.8 N`

Part b)

`\mu = 0.415`

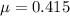
Step-by-step explanation:

Part a)

Time period of one revolution is given as

T = 42 s

now the angular speed of the belt is given as

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(42)`

`\omega = 0.15 rad/s`

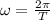
Now at rest position the force along the surface of carousel must be constant

so we will have

`mgsin\theta + m\omega^2 r cos\theta = F_f`

`30(9.81)sin20.5 + 30(0.15^2)(7.46)cos20.5 = F_f`

`F_f = 107.8 N`

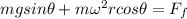
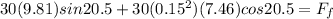
Part b)

New Time period of one revolution is given as

T = 30 s

now the angular speed of the belt is given as

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(30)`

`\omega = 0.21 rad/s`

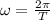
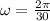
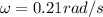
Now at rest position the force along the surface of carousel must be constant

so we will have

`mgsin\theta + m\omega^2 r cos\theta = F_f`

`30(9.81)sin20.5 + 30(0.21^2)(7.94)cos20.5 = F_f`

`F_f = 112.9 N`

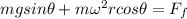
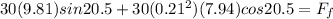
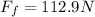
Also we know that in perpendicular direction also force is balanced

`F_n + m\omega^2 r sin\theta = mgcos\theta`

`F_n = mgcos\theta - m\omega^2 r sin\theta`

`F_n = 30(9.81)cos20.5 - 30(0.21)^2(7.94)sin20.5`

`F_n = 272 N`

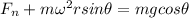
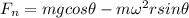
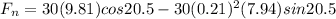
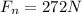
now for friction coefficient we will have

`F_f = \mu F_n`

`112.9 = \mu 272`

`\mu = 0.415`