Answer:
Option B
Explanation:
we know that
The volume of the cone is equal to
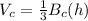
where
Bc is the area of the circle of the base of the cone
The volume of the square pyramid is equal to
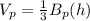
where
Bp is the area of the square base of the pyramid
we know that
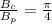
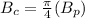
substitute in the formula of volume of the cone
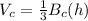
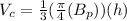
Remember that
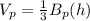
substitute
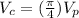 ----> StartFraction pi Over 4 EndFraction the volume of the pyramid
----> StartFraction pi Over 4 EndFraction the volume of the pyramid
or
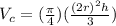 ----> StartFraction pi Over 4 EndFraction (StartFraction (2 r) squared (h) Over 3 EndFraction)
----> StartFraction pi Over 4 EndFraction (StartFraction (2 r) squared (h) Over 3 EndFraction)
or
 ----> One-thirdπr^2h
----> One-thirdπr^2h