Answer:
Acceleration of the plane, a = 5.4 g
Step-by-step explanation:
It is given that,
Speed of the jet plane, v = 1890 km/h = 525 m/s
Radius of the arc, r = 5.20 km = 5200 m
The plane is moving in the circular path, the centripetal acceleration will act on it. It is given by :
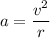
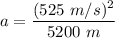
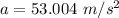
We know that, the value of g is,
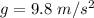
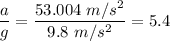
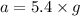
So, the acceleration of the plane is 5.4 g. Hence, this is the required solution.