Answer:
The final speed of the arrow when it hits the target is 45.63 m/s.
Step-by-step explanation:
Given;
spring constant of the bow, k = 458 N/m
extension of the bow, x = 0.72 m
mass of the arrow, m = 0.0925 kg
let the initial speed of the arrow after being fired = u
Apply the law of conservation of energy, the elastic potential energy of the bow will be converted to kinetic energy of the arrow.
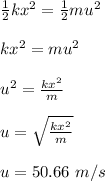
The speed of the arrow when it hits a target 24.7 m above the ground is calculated as;
v² = u² + 2gs
where;
v is the final speed when the arrow hits the target
g is acceleration due to gravity = (-9.8 m/s², upward motion)
v² = 50.66² + 2(-9.8)24.7
v² = 2566.44 - 484.12
v² = 2082.32
v = √2082.32
v = 45.63 m/s
Therefore, the final speed of the arrow when it hits the target is 45.63 m/s.