Question

Two horses start a race aat the same time. Horse A gallops at a steady rate of 32 feet per second and Horse B gallops at a steady rate of 28 feet per second.After 5 seconds, how much farther will Horse A have traveled?

Answer 1

Answer: 20 feet further

Answer 2

20 feet

Explanation:

The speed of horse A is
`S_(A)=32(feet)/(s)`

The speed of horse B is
`S_(B)=28(feet)/(s)`

We define the speed as distance divided by time.

Given that the horses started the race at the same time (and assuming in the same position) we can write :

`Speed=(Distance)/(Time) \\Distance=(Speed).(Time)`

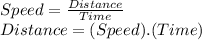
After 5 seconds for Horse A :

`Distance=(Speed).(Time)=(32(feet)/(s)).(5s)=160feet`

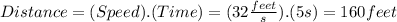
After 5 seconds, Horse A will have traveled 160 feet

After 5 seconds for Horse B :

`Distance=(Speed).(Time)=(28(feet)/(s)).(5s)=140feet`

After 5 seconds, Horse B will have traveled 140 feet

The difference between the distances :
`160feet-140feet=20feet`

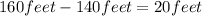
is how much farther Horse A will have traveled.

After 5 seconds, The Horse A will have traveled 20 feet farther than the Horse B.