Answer and explanation:
To prove :
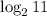 is irrational ?
is irrational ?
Proof :
Let
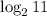 is rational number.
is rational number.
So, It can be expressed in p/q form where, p and q are integers and q is non-zero.

Using property of logarithm,
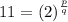
or
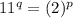
Which means 11 must be divisible by 2 for some p and q,
But 11 and 2 are co-prime.
So, Our assumption is not true.
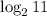 is irrational number.
is irrational number.
Hence proved.